Climb = what flat distance?
Comparing cycling routes
Your route sheet says today's ride is 127 miles with 6500 ft of climbing. Ummm, you wonder how that compares to the 145 miler with 3100 ft of climbing that you did last month. Which is harder? If only there was a way to compare the two. What is needed is a way to flatten each course in a way that accounts for the climbing, descending and wind. Then we could just compare the total equivalent flat distance (Total EFD) of any two routes to determine which is harder.
Let's be a little more precise. "Total EFD" is the distance that could be ridden on an entirely flat route in the same time as riding the actual (hilly or mountainous) route at the same power. Note that in both situations the rider's effort is identical, since power profiles and time are the same.
It turns out that this not a trivial problem and there is not a simple answer. One cannot say, for instance, that 1000 ft of climbing is equivalent to some constant number of flat miles. In fact, the equivalent flat distance of climbing (EFDC) depends on the rider's flat and climbing velocities, and the climbing distance of the course. Similarly, the equivalent flat distance of descending (EFDD) depends on the rider's flat and descending velocities, and descending distance of the course. Naturally, EFDC effectively lengthens the course and EFDD shortens it, so we must consider both to figure the Total equivalent flat distance (Total EFD).
In this article I'll provide a calculator that allows you to easily compare cycling routes, then I'll show graphs of some typical riders in various climbing and descending situations to illustrate how terrain and rider properties effectively lengthen or shorten a course. But first an overview.
Overview
Here is an illustration of our goal. We are given the length of course (D) and we wish to determine the Total Equivalent Flat Distance (Total EFD).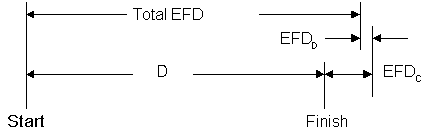
Figure 1: Depiction of the total equivalent flat distance (Total EFD)
Which is mathematically represented like this...
Total EFD = D + EFDC + EFDDwhere:
Total EFD = Total Equivalent Flat distance. This is the benchmark to compare diverse routes.
D = The measured distance of the route.
EFDC = Climbing Equivalent Flat distance. The extra flat distance that is equal to the route's climbing difficulty. In other words, if you flatten-out all the route's climbing, this is the flat distance that must be added to keep the finishing time the same.
EFDD = Descending Equivalent Flat distance. The flat distance that is equal to the route's descending. In other words, if you flatten-out all the route's descending, this is the flat distance that must be added to keep the finishing time the same. This should always be negative (adding a negative number is the same as subtracting), since descending should always be faster that riding on the flat.
Calculator: computes velocities, EFD and riding time
A software application computes rider velocities on the flats, climbs and descents based on the course, rider and environmental properties that you enter. Earlier work of Tom Compton provided inspiration and a material foundation. The calculator uses these velocities and the climbing and descending distances to compute the equivalent flat distance (EFD) of the course. Vary any property and see its effect on finishing time and equivalent flat distance!
EFD Java Web Start application - This link launches a separate application.
EFD Applet - This runs in your browser.
Excel spreadsheet - Downloads to your computer
Want to know more about how the ride calculator works? The equations it uses are provided.
Notes on using the calculator:
Estimate climbing and descending distances as 33% of the course length in the absence of better data. For instance, on a 100 mile course that starts and finishes at the same location, use 33 miles for both the climbing and descending distance.
Reduce both climbing and descending distances (not the elevations) calculated by your mapping software such as Delorme Topo USA by about 20%, thus increasing the average slope. For instance, on a 100 mile course with 47.5 miles of climbing and 45.2 miles of descending, use 38.0 miles [47.5 * (0.8)] and 36.2 miles [45.2 * (0.8)] for climbing and descending distances, respectively. This compensates for the bias of the shallowest slopes of the course.
Set descending power about 10 to 15% less than the flat power to account for inevitable coasting and soft pealing on the downhill portions. Make sure, however, that EFDD is stays negative, since descending should always shorten a course, not lengthen it.
Consider setting the climbing power equal to or slightly greater than the flat power.
Example
Let's look at our original question, which is harder: 127 miles with 6500
ft of climbing or 145 miles with 3100 ft of climbing. Let's assume that they
both start and finish in the same location (so the climbing and descending
elevations are the same), the climbing and descending distances are each 1/3
of the course length. Furthermore, we will use a typical
rider with a flat and climbing power of 125 watts and descending power
of 100 watts.
The 127 mile/6500 ft route is equivalent to 152.8 flat miles and takes 8:50 to complete. However, the 145 mile/3100 ft route is the same as 152.5 flat miles and takes 8:49 to finish. So for that rider two courses are almost exactly equivalent.
Graphical Representation
Let's look at a graphical view that provides a big picture view of this problem. How is course difficulty affected as the slope increases, rider power, or weight increases?
Here is a chart that shows the equivalent number of flat miles for each 1000 ft of climbing (FM1000) on a route for typical rider. These rider properties were varied where noted:

Figure 2: Number of miles equivalent to 1000 ft of climbing
This chart shows the number of flat miles that are added to a course due to 1000 ft of climbing. As you can see by the widely space curves, there is no magic number. That is, we cannot say that 1000 ft of climbing is equivalent to some constant number of flat miles for all situations. Instead it varies with the steepness of the slope and the power the rider applies on the uphill gradient.
For instance, a rider and bike weighing 87 kg (192 lbs) putting out 250 watts on a hill with a 4% average slope is equivalent to 3.7 flat miles for each 1000 ft climbed (FM1000 = 3.7 miles). But, the same rider applying half that power (125 watts) finds the same slope is equivalent to 6.9 flat miles per 1000 ft climbed.
Using the numbers from Tom Danielson's record setting 2004 Mt Evans hill climb this analysis revealed that Danielson retained 65% of his flat-speed in his blistering 1:41.20 ascent up the 27.2 mile / 6500 ft. mountain (4.5% average grade). However, a rider with the same size and weight applying only half of Danielson's power would retain only 50% of his flat-speed. With twice the power output, it is no surprise that Danielson's is much speedier on the flats (25.2 mph) and on the this climb (16.4 mph) then our hypothetical rider (19.6 mph and 9.7 mph respectively). However what is not so obvious, but nevertheless just as true, is that Danielson retains a much higher percentage of his flat-speed (65% vs. 50%) on the same grade.
Furthermore, it would take a 7% grade to slow Danielson to 49% of his flat-speed. So it takes a 7% grade to slow Danielson the same amount as a 4.5% grade slows our hypothetical rider (with half of Danielson's power). We can therefore conclude that a high power-to-weight ratio flattens a given course, and conversely a low power-to-weight ratio magnifies the apparent steepest of a grade.
Interestingly, riders applying the same power to weight ratio have similar FM1000 values for all slopes. Looking at the cyan and magenta curves in the above graph, the 87kg rider @ 150 watts and the 97kg rider @ 167.2 watts both have a power/weight ratio of 1.724 watts/kg and their curves are almost identical. That means that they are equally hindered by any given climb.
Now let's look at the effect of descending.

Figure 3: Chart showing number of miles equivalent to 1000 ft of descending
This chart shows the number of flat miles that are added to a course due to 1000 ft of descending (since the values are negative, descending subtracts miles). Comparing this figure with the previous, note that at any given slope climbing adds more miles that descending the same elevation gains back.
Counter-intuitively, a steeper descent gains back less distance than a shallower one and proportionally increases your riding time! This means your riding time will be significantly less (faster) if it included a descent of 1000 ft with a 1% slope than if had a descent of 1000 ft at 10%. How much faster? The course with the shallower downhill is 7 minutes and 8 seconds faster for the 87 kg rider @ 125 watts. The rider may go very fast down the steep hill, but is on the slope for a much short time, therefore, its effect on the average speed is less beneficial.
Taking this to a ridiculous extreme, when the slope is infinite (a cliff) the rider travels the minimum distance during the descent. The free fall may have been an exhilarating rush, but after a 1000 ft drop that rider is only 5 ft closer to the finish line (still has 999,995 ft to the finish line). The entire elevation drop was, in effect, wasted. However, the rider that descends 1000 ft on the 1% slope travels 100,000 ft from start to finish enjoying the benefit of the gradient over the entire course.
Furthermore, there is less variation between the descending riders than the same group climbing (comparing figures 2 and 3). This is especially true at the larger slopes. Thus increasing your power on the descents will improve your time less than if you applied the same power for the same duration on the climbs. In other words, if you want to get to the finish line sooner, save it for the climbs!
Conclusions
Here is a summary of the important take-away points remember:
» The equivalent flat distance for a given climbing elevation varies with slope of the climb and the power the rider applies. In other words, there is no constant (number of miles for each 1000 ft. of elevation gain) that can be used for all riders and gradients.
» For any given climbing elevation, steeper slopes hinder the rider more than shallower gradients. Note: hinder means the riding time is greater (slower) and the equivalent flat distance is longer by the same proportion.
» For any given slope and climbing elevation, a rider applying less power is hindered more by the climb than the same rider applying more power. For instance, a world-class climber like Tom Danielson maintains 50% of flat-speed on a 7% slope, but it takes only a 4.5% grade to reduce an otherwise identical rider except with half of Danielson's power to maintain the same percentage of his flat-speed.
» For any given slope and climbing elevation, two riders applying the same power to weight ratio are hindered nearly equally on climbs, especially the steeper ones.
» Climbing adds more time (slows a rider) than descending the same elevation gains back.
» Given the same descending elevation, shallower slopes help a rider more that steeper slopes. In other words, a rider is faster on a course that has longer and shallower descents than shorter and steeper ones. Note: help means the riding time is quicker and the equivalent flat distance is shorter by the same proportion.
Increasing your power on a climb will improve your time more than appling the same power for the same duration on a descent. In other words, to get to the finish line sooner, save it for the climbs. But, is it better to apply more power on level ground or on a climb? The answer to that question is here.
Rider properties
The following properties where used in the examples on this page except where
noted.
| Parameter | Value |
| W | 87 kg (192 lb. = 170 lb. rider + 18 lb. bike + 4 lb. water, gear, etc.) |
| Area* | 0.6934 m |
| CoefDrag | 0.5 |
| Dair | 1.226 kg/m |
| CoefRoll | 0.004 (asphalt) |
| Wind | 0 km/hr |
* Note: this area value was derived from known power measurements using a PowerTap device.
Additional references:
http://www.analyticcycling.com
http://home.hia.no/~stephens/aero.htm
www.abcc.co.uk/powertrain1.html

